Abstract
This paper develops a theory of optimal unemployment insurance (UI) in matching models. The optimal UI replacement rate is the conventional Baily-Chetty replacement rate, which solves the tradeoff between insurance and job-search incentives, plus a correction term, which is positive when an increase in UI pushes the labor market tightness toward its efficient level. In matching models, most wage mechanisms do not ensure efficiency, so tightness is generally inefficient. The effect of UI on tightness depends on the model: increasing UI may raise tightness by alleviating the rat race for jobs or lower tightness by increasing wages through bargaining.
Figure 4A: UI lowers labor market tightness in standard matching model
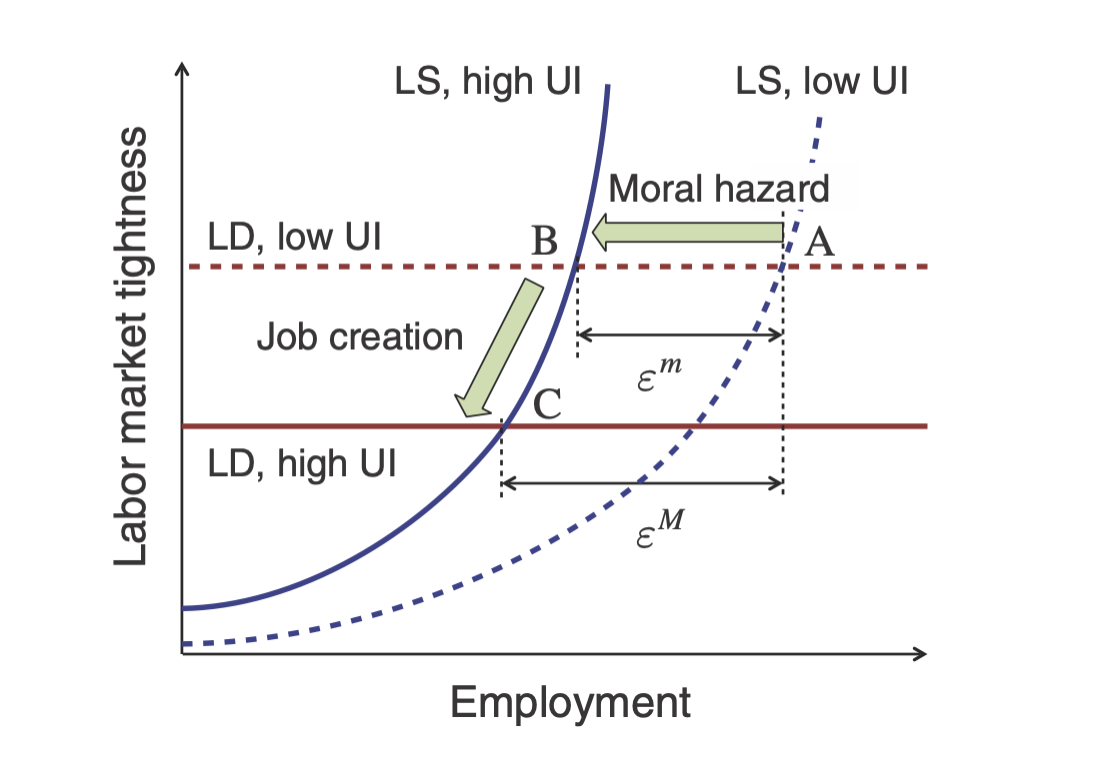
Figure 4B: UI has no effect on labor market tightness in fixed-wage model
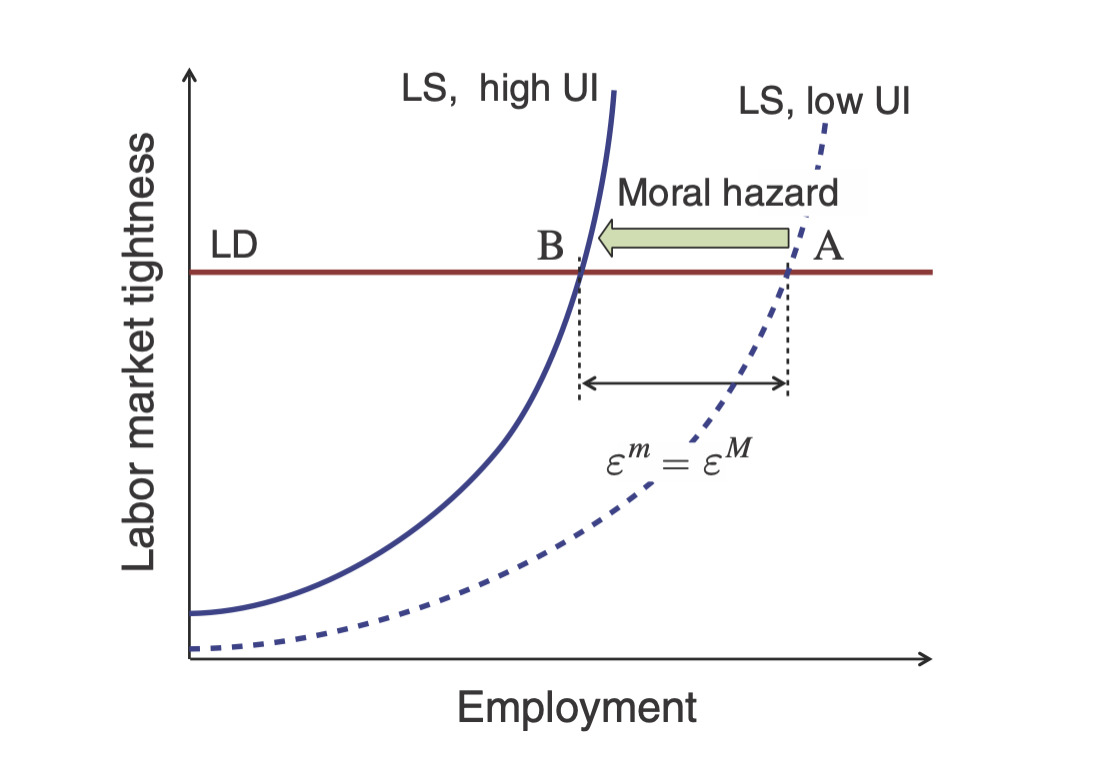
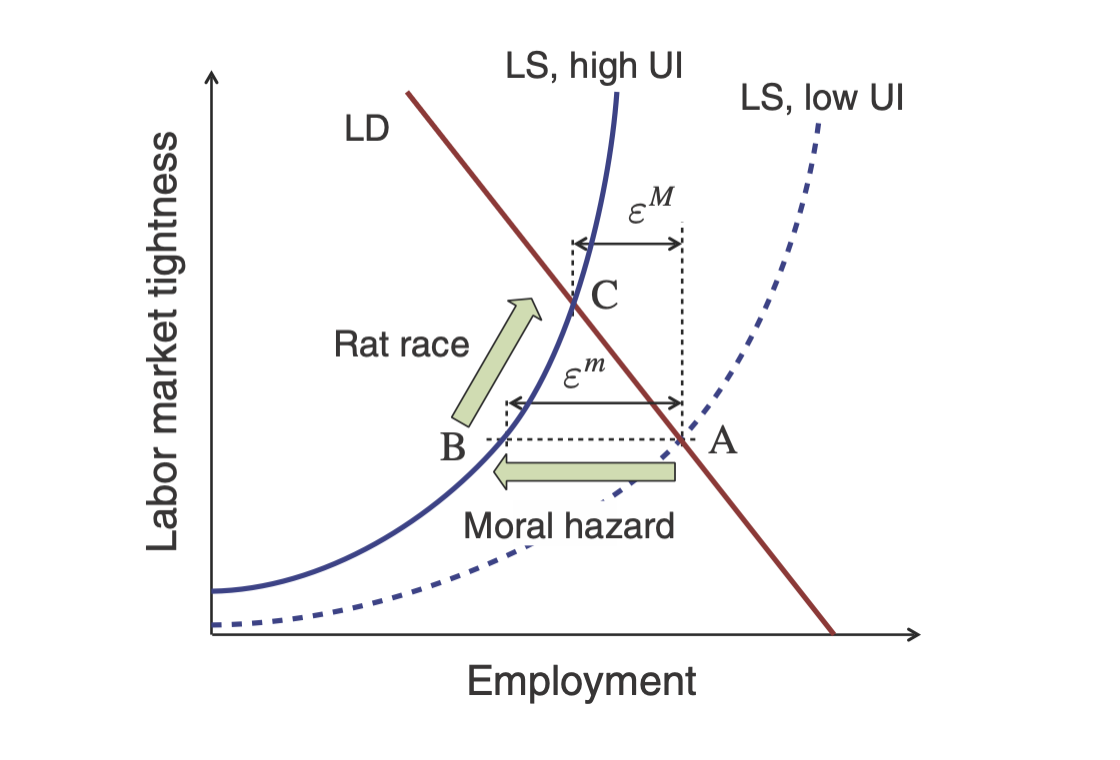
Figure 4C: UI raises labor market tightness in job-rationing model
Citation
Landais, Camille, Pascal Michaillat, and Emmanuel Saez. 2018. “A Macroeconomic Approach to Optimal Unemployment Insurance: Theory.” American Economic Journal: Economic Policy 10 (2): 152–181. https://doi.org/10.1257/pol.20150088 .
@article{LMS18,
author = {Camille Landais and Pascal Michaillat and Emmanuel Saez},
year = {2018},
title = {A Macroeconomic Approach to Optimal Unemployment Insurance: Theory},
journal = {American Economic Journal: Economic Policy},
volume = {10},
number = {2},
pages = {152--181},
url = {https://doi.org/10.1257/pol.20150088}}