Abstract
P-hacking is prevalent in reality but absent from classical hypothesis-testing theory. We therefore build a model of hypothesis testing that accounts for p-hacking. From the model, we derive critical values such that, if they are used to determine significance, and if p-hacking adjusts to the new significance standards, spurious significant results do not occur more often than intended. Because of p-hacking, such robust critical values are larger than classical critical values. In the model calibrated to medical science, the robust critical value is the classical critical value for the same test statistic but with one fifth of the significance level.
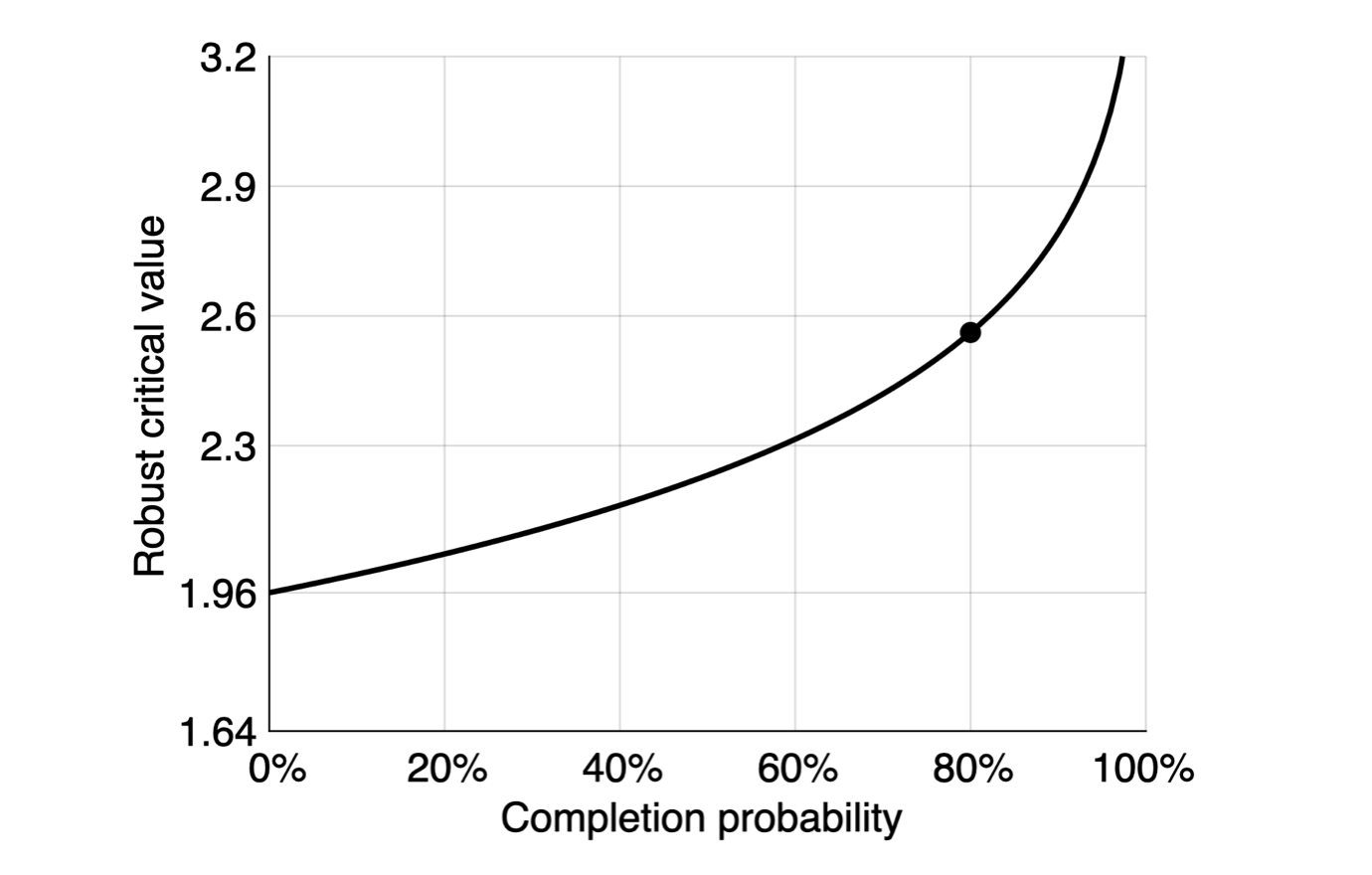
Figure 3A: Critical values robust to p-hacking for one-sided z-test with significance level of 5%

Figure 3B: Critical values robust to p-hacking for two-sided z-test with significance level of 5%
Citation
McCloskey, Adam, and Pascal Michaillat. 2024. “Critical Values Robust to P-hacking.” Review of Economics and Statistics. https://doi.org/10.1162/rest_a_01456.
@article{MM24,
author = {Adam McCloskey and Pascal Michaillat},
year = {2024},
title = {Critical Values Robust to P-hacking},
journal = {Review of Economics and Statistics},
url = {https://doi.org/10.1162/rest_a_01456}}